| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 4.1 | Exercise 4.2 | Exercise 4.3 |
| Exercise 4.4 | Exercise 4.5 | Exercise 4.6 |
Chapter 4 Basic Geometrical Ideas
Chapter 4, "Basic Geometrical Ideas," introduces students to the fundamental elements of geometry. The solutions page for this chapter provides clarity on concepts like points, lines, line segments, rays, intersecting lines, parallel lines, curves (open and closed), polygons, angles, triangles, quadrilaterals, and circles.
The solutions focus on helping students identify, name, and differentiate between these basic geometric entities. Exercises often involve identifying points, line segments, and rays within a given figure, and the solutions demonstrate the correct notation and terminology. The distinction between a line (extending infinitely in both directions), a line segment (having two endpoints), and a ray (having one endpoint and extending infinitely in one direction) is clarified through solved examples. Solutions explain the concepts of intersecting lines (meeting at a point) and parallel lines (never meeting).
The classification of curves as open or closed is illustrated, leading to the definition of polygons as simple closed curves made entirely of line segments. Solutions help identify vertices, sides, adjacent sides, adjacent vertices, and diagonals of polygons.
Special attention is given to angles, where solutions guide students in naming angles, identifying their vertex and arms, and locating points in the interior or exterior of an angle. Triangles and quadrilaterals are introduced as specific types of polygons, and solutions help identify their sides, angles, and vertices.
The basic components of a circle – center, radius, diameter, chord, arc, sector, segment, circumference, interior, and exterior – are explained, with solutions clarifying their definitions and relationships (e.g., diameter is twice the radius).
The solutions primarily focus on conceptual understanding and correct terminology rather than complex calculations, using diagrams effectively to illustrate the concepts. This chapter builds the essential vocabulary and spatial understanding needed for more advanced geometry.
Exercise 4.1
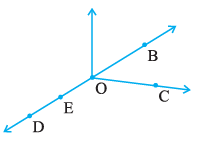
Question 1. Use the figure to name :
(a) Five points
(b) A line
(c) Four rays
(d) Five line segments
Answer:
(a) Five points
Based on the typical representation in such figures, the five points can be named as: D, E, O, B, C.
(b) A line
A line shown in the figure can be named as $\overleftrightarrow{DB}$. It can also be named using any two points on the line, such as $\overleftrightarrow{DE}$, $\overleftrightarrow{DO}$, $\overleftrightarrow{EB}$, $\overleftrightarrow{EO}$, or $\overleftrightarrow{OB}$.
(c) Four rays
Four rays shown in the figure can be named as:
$\overrightarrow{OD}$ (Ray starting from O going towards D)
$\overrightarrow{OE}$ (Ray starting from O going towards E)
$\overrightarrow{OC}$ (Ray starting from O going towards C)
$\overrightarrow{OB}$ (Ray starting from O going towards B)
(Other possible rays include $\overrightarrow{EB}$, $\overrightarrow{DB}$, etc.)
(d) Five line segments
Five line segments shown in the figure can be named as:
$\overline{DE}$ (Segment between D and E)
$\overline{EO}$ (Segment between E and O)
$\overline{OB}$ (Segment between O and B)
$\overline{OC}$ (Segment between O and C)
$\overline{DO}$ (Segment between D and O)
(Other possible segments include $\overline{DB}$, $\overline{EB}$, $\overline{EC}$, etc.)
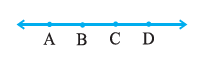
Question 2. Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.
Answer:
A line can be named by choosing any two distinct points on it. Since there are four points (A, B, C, and D) on the given line, we can form pairs of these points to name the line. The question asks for all twelve possible ways, which means we consider both orders for each pair of points (e.g., AB and BA are two different ways to name the same line).
The twelve possible names for the line are as follows:
1. $\overleftrightarrow{AB}$
2. $\overleftrightarrow{BA}$
3. $\overleftrightarrow{AC}$
4. $\overleftrightarrow{CA}$
5. $\overleftrightarrow{AD}$
6. $\overleftrightarrow{DA}$
7. $\overleftrightarrow{BC}$
8. $\overleftrightarrow{CB}$
9. $\overleftrightarrow{BD}$
10. $\overleftrightarrow{DB}$
11. $\overleftrightarrow{CD}$
12. $\overleftrightarrow{DC}$
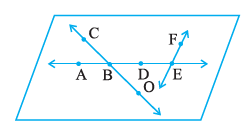
Question 3. Use the figure to name :
(a) Line containing point E.
(b) Line passing through A.
(c) Line on which O lies.
(d) Two pairs of intersecting lines.
Answer:
(a) Line containing point E.
There are two lines shown in the figure that contain point E.
One is the horizontal line, which can be named as $\overleftrightarrow{AE}$ or $\overleftrightarrow{DE}$.
The other is the slanted line, which can be named as $\overleftrightarrow{FE}$.
(b) Line passing through A.
The line passing through point A is the horizontal line $\overleftrightarrow{AE}$. It can also be named as $\overleftrightarrow{AD}$ or $\overleftrightarrow{AB}$.
(c) Line on which O lies.
The line on which point O lies is $\overleftrightarrow{CO}$. It can also be named as $\overleftrightarrow{CB}$.
(d) Two pairs of intersecting lines.
Two pairs of intersecting lines from the figure are:
1. The lines $\overleftrightarrow{AE}$ and $\overleftrightarrow{CO}$. They intersect at point B.
2. The lines $\overleftrightarrow{AE}$ and $\overleftrightarrow{FE}$. They intersect at point E.
Question 4. How many lines can pass through
(a) one given point?
(b) two given points?
Answer:
(a) one given point?
An infinite number of lines can pass through one given point.
(b) two given points?
Exactly one line can pass through two given distinct points.
Question 5. Draw a rough figure and label suitably in each of the following cases:
(a) Point P lies on $\overline{AB}$.
(b) $\overleftrightarrow{XY}$ and $\overleftrightarrow{PQ}$ intersect at M.
(c) Line l contains E and F but not D.
(d) $\overleftrightarrow{OP}$ and $\overleftrightarrow{OQ}$ meet at O.
Answer:
(a) Point P lies on $\overline{AB}$.
A rough figure showing point P lying on the line segment $\overline{AB}$ is as follows:
(b) $\overleftrightarrow{XY}$ and $\overleftrightarrow{PQ}$ intersect at M.
A rough figure showing two lines $\overleftrightarrow{XY}$ and $\overleftrightarrow{PQ}$ intersecting at point M is as follows:
(c) Line l contains E and F but not D.
A rough figure showing line l containing points E and F, but not point D, is as follows:
(d) $\overleftrightarrow{OP}$ and $\overleftrightarrow{OQ}$ meet at O.
A rough figure showing two lines $\overleftrightarrow{OP}$ and $\overleftrightarrow{OQ}$ meeting at point O is as follows:
Question 6. Consider the following figure of line $\overleftrightarrow{MN}$ . Say whether following statements are true or false in context of the given figure.
(a) Q, M, O, N, P are points on the line $\overleftrightarrow{MN}$.
(b) M, O, N are points on a line segment $\overline{MN}$ .
(c) M and N are end points of line segment $\overline{MN}$ .
(d) O and N are end points of line segment $\overline{OP}$ .
(e) M is one of the end points of line segment $\overline{QO}$ .
(f) M is point on ray $\overrightarrow{OP}$ .
(g) Ray $\overrightarrow{OP}$ is different from ray $\overrightarrow{OP}$ .
(h) Ray $\overrightarrow{OP}$ is same as ray $\overrightarrow{OM}$ .
(i) Ray $\overrightarrow{OM}$ is not opposite to ray $\overrightarrow{OP}$.
(j) O is not an initial point of $\overrightarrow{OP}$ .
(k) N is the initial point of $\overrightarrow{NP}$ and $\overrightarrow{NM}$ .
.Answer:
Assuming the points Q, M, O, N, P lie on the line $\overleftrightarrow{MN}$ in that order from left to right.
(a) Q, M, O, N, P are points on the line $\overleftrightarrow{MN}$.
True. The figure shows all these points lying on the line.
(b) M, O, N are points on a line segment $\overline{MN}$.
True. The line segment $\overline{MN}$ includes the endpoints M and N and all points between them. O is between M and N.
(c) M and N are end points of line segment $\overline{MN}$.
True. By definition, the endpoints of line segment $\overline{MN}$ are M and N.
(d) O and N are end points of line segment $\overline{OP}$.
False. The endpoints of line segment $\overline{OP}$ are O and P.
(e) M is one of the end points of line segment $\overline{QO}$.
False. The endpoints of line segment $\overline{QO}$ are Q and O. M lies between Q and O.
(f) M is point on ray $\overrightarrow{OP}$.
False. Ray $\overrightarrow{OP}$ starts at O and extends towards P (to the right). Point M is to the left of O, so it is not on ray $\overrightarrow{OP}$.
(g) Ray $\overrightarrow{OP}$ is different from ray $\overrightarrow{QP}$.
True. Ray $\overrightarrow{OP}$ starts at O, while ray $\overrightarrow{QP}$ starts at Q. Since they have different starting points, they are different rays.
(h) Ray $\overrightarrow{OP}$ is same as ray $\overrightarrow{OM}$.
False. Both rays start at O, but they extend in opposite directions. $\overrightarrow{OP}$ goes right, and $\overrightarrow{OM}$ goes left.
(i) Ray $\overrightarrow{OM}$ is not opposite to ray $\overrightarrow{OP}$.
False. Ray $\overrightarrow{OM}$ and ray $\overrightarrow{OP}$ start at the same point O and extend in exactly opposite directions along the line. Therefore, they are opposite rays.
(j) O is not an initial point of $\overrightarrow{OP}$.
False. By definition, the initial point (starting point) of ray $\overrightarrow{OP}$ is O.
(k) N is the initial point of $\overrightarrow{NP}$ and $\overrightarrow{NM}$.
True. Ray $\overrightarrow{NP}$ starts at N and goes towards P. Ray $\overrightarrow{NM}$ starts at N and goes towards M. In both cases, N is the initial point.
Exercise 4.2
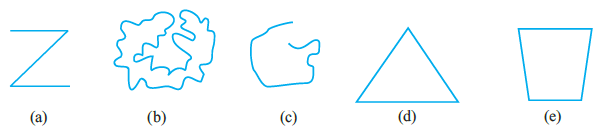
Question 1. Classify the following curves as (i) Open or (ii) Closed.
Answer:
We classify the curves based on whether their endpoints meet.
(a)
The curve does not end where it started. It has distinct starting and ending points.
Therefore, it is an Open curve.
(b)
The curve starts and ends at the same point, enclosing a region.
Therefore, it is a Closed curve.
(c)
The curve has distinct starting and ending points and does not form a loop.
Therefore, it is an Open curve.
(d)
The curve is made of line segments that start and end at the same point (forming a triangle).
Therefore, it is a Closed curve.
(e)
The curve is made of line segments that start and end at the same point (forming a polygon).
Therefore, it is a Closed curve.
Question 2. Draw rough diagrams to illustrate the following :
(a) Open curve
(b) Closed curve.
Answer:
(a) Open curve
An open curve is a curve where the start and end points are different. Below is a rough diagram of an open curve.
(b) Closed curve
A closed curve is a curve that starts and ends at the same point, forming a complete loop. Below is a rough diagram of a closed curve.
Question 3. Draw any polygon and shade its interior.
Answer:
A polygon is a simple closed figure made up entirely of line segments. The area enclosed by the boundary of the polygon is called its interior.
Let's draw a five-sided polygon, which is known as a pentagon. We can name its vertices (corners) as A, B, C, D, and E.
The boundary of the pentagon is formed by the line segments $\overline{AB}$, $\overline{BC}$, $\overline{CD}$, $\overline{DE}$, and $\overline{EA}$.
Below is a rough diagram of the pentagon ABCDE with its interior shaded.
In the figure above:
- The points A, B, C, D, and E are the vertices of the polygon.
- The path formed by the line segments $\overline{AB}$, $\overline{BC}$, $\overline{CD}$, $\overline{DE}$, and $\overline{EA}$ is the boundary of the polygon.
- The shaded part represents the interior of the polygon.
Question 4. Consider the given figure and answer the questions :

(a) Is it a curve?
(b) Is it closed?
Answer:
(a) Is it a curve?
Yes, the given figure is a curve. In geometry, any drawing done without lifting the pencil can be considered a curve. This includes figures made of straight line segments.
(b) Is it closed?
Yes, the figure is a closed curve. It starts and ends at the same point, forming a boundary that encloses a region.
Question 5. Illustrate, if possible, each one of the following with a rough diagram:
(a) A closed curve that is not a polygon.
(b) An open curve made up entirely of line segments.
(c) A polygon with two sides.
Answer:
(a) A closed curve that is not a polygon.
A polygon must be a closed curve made up entirely of straight line segments. Therefore, any closed curve that has curved parts is not a polygon. A circle or an oval is a common example.
(b) An open curve made up entirely of line segments.
An open curve has different start and end points. This can be illustrated by connecting several line segments end-to-end without connecting the final end point back to the starting point.
(c) A polygon with two sides.
This is not possible to draw.
A polygon is a closed figure made of line segments. To form a closed figure, a minimum of three line segments are required. The simplest polygon is a triangle, which has three sides. Two line segments cannot enclose a space to form a closed figure.
Exercise 4.3
Question 1. Name the angles in the given figure.

Answer:
The figure shown is a quadrilateral named ABCD.
The angles in the given figure are formed at the vertices A, B, C, and D.
There are four angles in the figure:
1. $\angle DAB$ (or $\angle A$)
2. $\angle ABC$ (or $\angle B$)
3. $\angle BCD$ (or $\angle C$)
4. $\angle CDA$ (or $\angle D$)
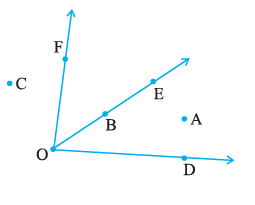
Question 2. In the given diagram, name the point(s)
(a) In the interior of ∠DOE
(b) In the exterior of ∠EOF
(c) On ∠EOF
Answer:
(a) In the interior of ∠DOE
The interior of $\angle DOE$ is the region between the rays $\overrightarrow{OD}$ and $\overrightarrow{OE}$.
Observing the figure, the point located in this region is A.
(b) In the exterior of ∠EOF
The exterior of $\angle EOF$ is the region outside the rays $\overrightarrow{OE}$ and $\overrightarrow{OF}$.
Observing the figure, the points located in the exterior are C, A, and D.
(c) On ∠EOF
The points on $\angle EOF$ are the points lying on the rays $\overrightarrow{OE}$ or $\overrightarrow{OF}$.
Observing the figure, the points on the angle are E, O, B, and F.
Question 3. Draw rough diagrams of two angles such that they have
(a) One point in common.
(b) Two points in common.
(c) Three points in common.
(d) Four points in common.
(e) One ray in common.
Answer:
(a) One point in common.
Two angles can have only one point in common if they share only their vertex. For example, in the diagram below, $\angle AOB$ and $\angle COD$ have only point O in common.
(b) Two points in common.
Two angles can have two points in common if they share a common vertex and another point on a common arm (ray). In the diagram below, $\angle AOB$ and $\angle BOC$ share the vertex O and the point P which lies on their common ray $\overrightarrow{OB}$.
(c) Three points in common.
Two angles can have three points in common if they share a common vertex and two other points on a common arm. In the diagram below, $\angle PQR$ and $\angle SQR$ share the vertex Q and two other points, A and B, which lie on their common ray $\overrightarrow{QR}$.
(d) Four points in common.
Two angles can have four points in common if they share a common vertex and three other points on a common arm. In the diagram below, $\angle AOB$ and $\angle COB$ share the vertex O and three other points, X, Y, and Z, which lie on their common ray $\overrightarrow{OB}$.
(e) One ray in common.
Two angles have one ray in common if they are adjacent angles. In the diagram below, $\angle AOB$ and $\angle BOC$ are adjacent angles. They have the ray $\overrightarrow{OB}$ as their common arm.
Exercise 4.4
Question 1. Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior?
Answer:
A rough sketch of a triangle ABC is drawn below. A triangle is a three-sided polygon. The region enclosed by the boundary of the triangle is called its interior, and the region outside the boundary is its exterior.
In the sketch, point P is marked in the interior of the triangle, and point Q is marked in its exterior.
The question is whether point A is in the exterior or in the interior of the triangle.
A point's location relative to a triangle can be:
- In the interior (inside the figure)
- In the exterior (outside the figure)
- On the boundary of the figure
Point A is a vertex of the triangle ABC. A vertex is a point where two sides of the triangle meet, which means it is part of the boundary of the triangle.
Therefore, the point A lies on the triangle; it is neither in the interior nor in the exterior.
Question 2.
(a) Identify three triangles in the figure.
(b) Write the names of seven angles.
(c) Write the names of six line segments.
(d) Which two triangles have ∠B as common?

Answer:
Based on the figure where a line segment is drawn from vertex A to a point D on the opposite side BC:
(a) Identify three triangles in the figure.
The three triangles visible in the figure are:
1. The large triangle: $\triangle ABC$
2. The left-side triangle: $\triangle ABD$
3. The right-side triangle: $\triangle ADC$
(b) Write the names of seven angles.
The seven angles in the figure are:
1. $\angle ABC$ (or $\angle B$)
2. $\angle ACB$ (or $\angle C$)
3. $\angle BAC$ (the entire angle at vertex A)
4. $\angle BAD$ (the left part of the angle at vertex A)
5. $\angle CAD$ (the right part of the angle at vertex A)
6. $\angle ADB$ (angle at D in $\triangle ABD$)
7. $\angle ADC$ (angle at D in $\triangle ADC$)
(c) Write the names of six line segments.
The six line segments in the figure are:
1. $\overline{AB}$
2. $\overline{AC}$
3. $\overline{BC}$
4. $\overline{AD}$
5. $\overline{BD}$
6. $\overline{DC}$
(d) Which two triangles have ∠B as common?
The angle $\angle B$ is part of the large triangle $\triangle ABC$ and also part of the smaller triangle $\triangle ABD$.
Therefore, the two triangles that have $\angle B$ as a common angle are $\triangle ABC$ and $\triangle ABD$.
Exercise 4.5
Question 1. Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?
Answer:
A rough sketch of a quadrilateral PQRS and its diagonals is shown below.
Naming the Diagonals:
The diagonals are the line segments that connect opposite vertices.
The two diagonals in the quadrilateral PQRS are: $\overline{PR}$ and $\overline{QS}$.
Location of the Meeting Point:
As seen in the figure, the diagonals $\overline{PR}$ and $\overline{QS}$ cross each other at a point that is inside the boundary of the quadrilateral.
Therefore, the meeting point of the diagonals is in the interior of the quadrilateral PQRS.
Question 2. Draw a rough sketch of a quadrilateral KLMN. State,
(a) two pairs of opposite sides,
(b) two pairs of opposite angles,
(c) two pairs of adjacent sides,
(d) two pairs of adjacent angles.
Answer:
A rough sketch of a quadrilateral KLMN is shown below to help identify its parts.
(a) two pairs of opposite sides
Opposite sides are sides that do not share a common vertex.
The two pairs of opposite sides are:
1. $\overline{KL}$ and $\overline{NM}$
2. $\overline{KN}$ and $\overline{LM}$
(b) two pairs of opposite angles
Opposite angles are angles at vertices that are not adjacent.
The two pairs of opposite angles are:
1. $\angle K$ (or $\angle LKN$) and $\angle M$ (or $\angle NML$)
2. $\angle L$ (or $\angle KLM$) and $\angle N$ (or $\angle KNM$)
(c) two pairs of adjacent sides
Adjacent sides are sides that share a common vertex.
Two examples of adjacent sides are:
1. $\overline{KL}$ and $\overline{LM}$ (they meet at vertex L)
2. $\overline{LM}$ and $\overline{MN}$ (they meet at vertex M)
(Other pairs are ($\overline{MN}$, $\overline{NK}$) and ($\overline{NK}$, $\overline{KL}$)).
(d) two pairs of adjacent angles
Adjacent angles are angles whose vertices are the endpoints of the same side.
Two examples of adjacent angles are:
1. $\angle K$ and $\angle L$ (they are at the ends of side $\overline{KL}$)
2. $\angle L$ and $\angle M$ (they are at the ends of side $\overline{LM}$)
(Other pairs are ($\angle M$, $\angle N$) and ($\angle N$, $\angle K$)).
Question 3. Investigate:
Use strips and fasteners to make a triangle and a quadrilateral.
Try to push inward at any one vertex of the triangle. Do the same to the quadrilateral.
Is the triangle distorted? Is the quadrilateral distorted? Is the triangle rigid?
Why is it that structures like electric towers make use of triangular shapes and not quadrilaterals?
Answer:
Investigation Results:
When we make a triangle and a quadrilateral using strips and fasteners and apply pressure at a vertex, we observe the following:
For the Triangle:
When you push inward at any vertex of the triangle, its shape does not change. The lengths of the sides fix the angles, making the structure strong and resistant to deformation.
For the Quadrilateral:
When you push inward at any vertex of the quadrilateral, its shape changes easily. The angles are not fixed, and it can be skewed into different shapes like a rhombus or other parallelograms.
Answers to the Questions:
Is the triangle distorted? No, the triangle is not distorted.
Is the quadrilateral distorted? Yes, the quadrilateral is easily distorted.
Is the triangle rigid? Yes, the triangle is a rigid figure.
Application in Structures:
Structures like electric towers, bridges, and cranes require great strength and stability. Since triangles are rigid and do not change their shape under pressure, they are fundamental to building strong and stable structures. By arranging triangles in a framework (a truss), the structure can withstand strong forces like wind and heavy loads without collapsing. A quadrilateral lacks this natural rigidity, which is why triangular shapes are preferred in engineering for creating strong frameworks.
Exercise 4.6

Question 1. From the figure, identify :
(a) the centre of circle
(b) three radii
(c) a diameter
(d) a chord
(e) two points in the interior
(f) a point in the exterior
(g) a sector
(h) a segment
Answer:
Based on the typical components shown in diagrams for such questions:
(a) the centre of circle
The centre of the circle is point O.
(b) three radii
A radius is a line segment connecting the centre to a point on the circle. Three radii shown are:
$\overline{OA}$
$\overline{OB}$
$\overline{OC}$
(c) a diameter
A diameter is a chord passing through the centre. It is the longest chord, equal to twice the radius.
The diameter shown is $\overline{AC}$.
(d) a chord
A chord is a line segment whose endpoints lie on the circle.
A chord shown is $\overline{ED}$.
(Note: The diameter $\overline{AC}$ is also a chord.)
(e) two points in the interior
Points in the interior are points inside the boundary of the circle.
Two points in the interior are O (the centre) and P.
(f) a point in the exterior
A point in the exterior is a point outside the boundary of the circle.
A point in the exterior is Q.
(g) a sector
A sector is the region in the interior of the circle enclosed by an arc and two radii connecting the centre to the endpoints of the arc.
The shaded region between radii $\overline{OA}$ and $\overline{OB}$ is a sector (specifically, sector AOB).
(h) a segment
A segment is the region in the interior of the circle enclosed by a chord and the arc subtended by the chord.
The region enclosed by the chord $\overline{ED}$ and the arc ED (shaded in the figure) is a segment.
Question 2.
(a) Is every diameter of a circle also a chord?
(b) Is every chord of a circle also a diameter?
Answer:
(a) Is every diameter of a circle also a chord?
Yes.
Reasoning: A chord is a line segment whose endpoints lie on the circle. A diameter is a line segment that connects two points on the circle and passes through the centre. Since the endpoints of a diameter lie on the circle, it satisfies the definition of a chord.
(b) Is every chord of a circle also a diameter?
No.
Reasoning: A chord only needs its endpoints to be on the circle. A diameter is a special type of chord that must pass through the centre of the circle. Many chords can be drawn that do not pass through the centre. Therefore, not every chord is a diameter.
Question 3. Draw any circle and mark
(a) its centre
(b) a radius
(c) a diameter
(d) a sector
(e) a segment
(f) a point in its interior
(g) a point in its exterior
(h) an arc
Answer:
Below is a rough diagram of a circle with all the requested parts marked and labeled:
Here is an explanation of the parts marked in the figure:
(a) its centre: Point O is the centre of the circle.
(b) a radius: The line segment $\overline{OA}$, which connects the centre to a point on the circle, is a radius.
(c) a diameter: The line segment $\overline{BC}$, which passes through the centre and has its endpoints on the circle, is a diameter.
(d) a sector: The shaded region enclosed by two radii ($\overline{OA}$ and $\overline{OD}$) and the arc between them ($\overset{\frown}{AD}$) is a sector.
(e) a segment: The shaded region enclosed by a chord ($\overline{DE}$) and the arc above it ($\overset{\frown}{DE}$) is a segment.
(f) a point in its interior: Point P is located inside the circle, so it is in the interior.
(g) a point in its exterior: Point Q is located outside the circle, so it is in the exterior.
(h) an arc: The portion of the circle's boundary between points D and E, denoted as $\overset{\frown}{DE}$, is an arc.
Question 4. Say true or false :
(a) Two diameters of a circle will necessarily intersect.
(b) The centre of a circle is always in its interior.
Answer:
(a) Two diameters of a circle will necessarily intersect.
True.
Reasoning: By definition, every diameter of a circle must pass through the centre of the circle. Since both diameters pass through the same single point (the centre), they must intersect at that point.
(b) The centre of a circle is always in its interior.
True.
Reasoning: The interior of a circle consists of all points whose distance from the centre is less than the radius. The centre's distance from itself is 0, which is always less than the radius (which must be a positive value). Therefore, the centre lies within the interior of the circle.

